Circular Orbits | NemoQuiz

The orbits of planets in our solar system are elliptical.
(This is part of Kepler’s 1st law of planetary motion)

However, it’s fun to approximate with easier math by assuming that they’re circular.

A planet is held in a roughly circular orbit* by a centripetal force that pulls toward the center of its orbit. That force is the gravitational force between the star and the planet.
(*Actual orbits are elliptical. Taking earth as an example, at its farthest from the sun, earth is about 3% farther than it is at the closest approach in its orbit.)

F_c = F_g

We can substitute the equations for F_c and F_g into this equation as follows:

$\cfrac{{m_p}v^2}{r} = \cfrac{G{m_p}{m_s}}{r^2}$

Where:
m_p = mass of the planet (kg)
m_s = mass of the star (kg)
r = radius of the circular orbit (m)
v = velocity of the planet in its orbit (m/s)
G = gravitational constant = 6.67 x 10⁻¹¹ Nm²/kg²

Notice that in the left side (centripetal force equation), we use the mass of the planet since that’s the mass that’s being accelerated around in a circle. Also note that the radius, r, is the radius of the circular orbit. It is NOT the radius of the planet or star.

The mass of the planet cancels out, and we also cancel out one radius from each side to give this:

$v^2 = \cfrac{G{m_s}}{r}$

And taking the square root of both sides, we get an equation for velocity of a satellite in a circular orbit around a central mass, m:

$v = \sqrt{\cfrac{Gm}{r}}$

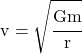
For a planet going around a star, m is the mass of the star.
For a moon going around a planet, m is the mass of the planet.
Either way, m is the central mass, and r is always the radius of the circular orbit.

Kepler’s 3rd Law

This same equation leads to Kepler’s 3rd law, which for a circular orbit would read as follows:

The period (T) of a planet squared is proportional to the orbital radius cubed.

In simpler terms: the farther away a planet is from the sun, the longer its year is. (Example: a Jupiter year is about 12 earth years)

In mathematical terms:

$T^2 \propto r^3$

We can get that using an equation relating velocity, v, to period, T:

$v = \cfrac{2\pi r}{T}$

Substituting that into the orbit equation and rearranging:

$(2 \pi)^2 r^3 = GmT^2$

We can see r³ on the left and T² on the right. Isaac Newton knew Kepler’s laws when he was studying gravitation, and he was able to work backwards from Kepler’s 3rd Law to discover the inverse square law for universal gravitation.