Equations

Kinematics

$\bar{v} = \cfrac{\Delta x}{\Delta t}$

$\Delta v = v - v_0$

$\bar{v} = \cfrac{v + v_0}{2}$

$\Delta x = (\cfrac{v + v_0}{2}) \Delta t$

$a = \cfrac{\Delta v}{\Delta t}$

$v = v_0 + at$

$\Delta x = {v_0}t + \cfrac{1}{2}at^2$

$v^2 = {v_0}^2 + 2a\Delta x$

$g = \SI{10}{m \per s^2}$

Force

$a = \cfrac{F_{net}}{m}$

$W = F_g = mg$

$F_F = \mu F_N$

Energy

$W = Fd$

$P = \cfrac{W}{\Delta t} = \cfrac{Fd}{\Delta t} = Fv$

$E_k = \cfrac{1}{2}mv^2$

$E_g = mgh$

$E_s = \cfrac{1}{2}kx^2$

$Efficiency = \cfrac{P_{out}}{P_{in}} = \cfrac{W_{out}}{W_{in}}$

$g = \SI{10}{m \per s^2}$

Momentum

$p = mv$

${m_1}{v_1} + {m_2}{v_2} = {m_1}{v_1}^\prime + {m_2}{v_2}^\prime$

${m_1}{v_1} + {m_2}{v_2} = (m_1 + m_2){v}^\prime$

$J = \Delta p = m \Delta v = F \Delta t$

Gravitation & Circular Motion

$F_g = \cfrac{G m_1 m_2}{r^2}$

$g = \cfrac{G m}{r^2}$

$F_g = mg$

$G = 6.67 \times 10^{-11} \: \si{N m^2}/\si{kg^2}$

$a_c = \cfrac{v^2}{r}$

$v = C \omega = 2\pi r \omega = \cfrac{C}{T}$

$\omega = 1 / T$

$C = 2 \pi r$

$v = \sqrt{\cfrac{Gm}{r}}$

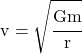
(ω must be in rev/s)

Simple Harmonic Motion

$T = \cfrac{1}{f}$

$T_p = 2 \pi \sqrt{\cfrac{\ell}{g}}$

$T_s = 2 \pi \sqrt{\cfrac{m}{k}}$

$F_s = -kx$

$E_s = \cfrac{1}{2}kx^2$

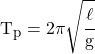
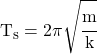
Torque & Angular Motion

$\theta = \cfrac{x}{r}$

$\omega = \cfrac{v}{r}$

$\alpha = \cfrac{a}{r}$

$\omega = \cfrac{\Delta\theta}{\Delta t}$

$\alpha = \cfrac{\Delta\omega}{\Delta t}$

$\theta = \theta_0 + \omega_0 t + \cfrac{1}{2}\alpha t^2$

$\omega = \omega_0 + \alpha t$

$\omega^2 = \omega_0^2 + 2\alpha\Delta\theta$

$\tau = Fr$

$\tau_{net} = I\alpha$

$L = I\omega$

$\Delta L = \tau \Delta t$

$K = \cfrac{1}{2}I \omega^2$

Moment of Inertia Equations

Point Mass: $I = MR^2$

Solid Sphere: $I = \cfrac{2}{5}MR^2$

Hollow Sphere: $I = \cfrac{2}{3}MR^2$

Solid Cylinder: $I = \cfrac{1}{2}MR^2$ (symmetry axis)

Thin Hoop: $I = MR^2$ (symmetry axis)

Rotational Motion Symbols

$I = rotational \ inertia$

$K = kinetic \ energy$

$L = angular \ momentum$

$\alpha = angular \ acceleration$

$\theta = angle$

$\tau = torque$

$\omega = angular \ speed$

Electrical Forces and Fields

$F_E = \cfrac{k \lvert q_1 q_2 \rvert}{r^2}$

$E = \cfrac{k \lvert Q \rvert }{r^2}$

$F_E = qE$

$U_E = \cfrac{kqQ}{r}$

$V = \cfrac{kq}{r}$

$\Delta U_E = q \Delta V$

$E = \cfrac{\Delta V}{\Delta r}$

$k = 9.0 \times 10^9 \: \si{N m^2}/\si{C^2} = \cfrac{1}{4 \pi \epsilon_0}$

$e = 1.60 \times 10^{-19} \: \si{C}$

$m_{electron} = 9.11 \times 10^{-31} \: \si{kg}$

$m_{proton} = 1.67 \times 10^{-27} \: \si{kg}$

Electricity & Magnetism

$F_M = qvB \sin{\Theta}$

$F_M = I \ell \sin{\Theta}B$

$\Phi_B = B \cdot A$

$\epsilon = emf = \Delta V$

$\epsilon = \minus\cfrac{\Delta \Phi}{\Delta t}$

$\epsilon = B \ell v$

$B = \cfrac{\mu_0}{2 \pi}\cfrac{I}{r}$

$\mu_0 = 4 \pi \times 10^{-7}$

DC Circuits

$I = \cfrac{V}{R}$

$\Delta V = IR$

$P = I \Delta V = I^2 R = \cfrac{\Delta V^2}{R}$

$R_{eq} = R_1 + R_2 + R_3 + ...$

$\cfrac{1}{R_{eq}} = \cfrac{1}{R_1} + \cfrac{1}{R_2} + \cfrac{1}{R_3} + ...$

$I = \cfrac{\Delta Q}{\Delta t}$

$\Delta V = \cfrac{Q}{C}$

$R = \cfrac{\rho \ell}{A}$

$C = \kappa \epsilon_0 \cfrac{A}{d}$

$R_s = \sum\limits_i R_i$

$\cfrac{1}{R_p} = \sum\limits_i \cfrac{1}{R_i}$

$C_p = \sum\limits_i C_i$

$\cfrac{1}{C_s} = \sum\limits_i \cfrac{1}{C_i}$

$E = \cfrac{Q}{\epsilon_0 A}$

$U_C = \cfrac{1}{2}Q \Delta V = \cfrac{1}{2} C (\Delta V)^2$

Mechanical Waves and Sound

$v = \lambda f$

Waves on a string:
$v = \sqrt{\cfrac{F_T}{\mu}}$

$\mu = linear \: density \: (kg/m)$

$\mu = mass / length$

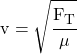
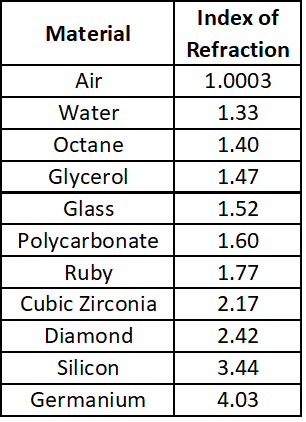
Light and Geometric Optics

c = 2.998 x 10⁸ m/s

$v = \lambda f$

$n = \cfrac{c}{v}$

$n_1 \sin\theta_1 = n_2 \sin\theta_2$

$d \sin\theta = m \lambda = \Delta \ell = 2t$

$\cfrac{1}{f} = \cfrac{1}{d_i} + \cfrac{1}{d_o}$

$\lvert M\rvert = \lvert\cfrac{d_i}{d_o}\rvert = \lvert\cfrac{h_i}{h_o}\rvert$

Fluid Mechanics

$\rho = \cfrac{m}{V}$

$P = \cfrac{F}{A}$

$P = P_0 + \rho gh$

$F_b = \rho V g$

$A_1 v_1 = A_2 v_2$

$P_1 + \rho g y_1 + \cfrac{1}{2} \rho v_1^2 = P_2 + \rho g y_2 + \cfrac{1}{2} \rho v_2^2$

$P_0 = 101325 \, \si{Pa}$

$1 \, \si{atm} = 101325 \, \si{Pa}$

Thermodynamics

$\Delta U = Q + W$

$W = -P \Delta V$

$PV = nRT$

$\cfrac{P_1 V_1}{T_1} = \cfrac{P_2 V_2}{T_2}$

$\cfrac{Q}{\Delta t} = \cfrac{kA \Delta T}{L}$

$KE = \cfrac{3}{2}k_B T$

$U = \cfrac{3}{2}nRT$

$R = 8.314 \, \cfrac{\si{\pascal \meter \cubed}}{\si{\mole \kelvin}}$

$k_B = \num{1.38 e-23} \, \cfrac{\si{\joule}}{\si{\kelvin}}$

Modern Physics

$c = \num{3.00 e8} \, \si{m/s}$

$h = \num{6.63 e-34} \, \si{J}\dot\si{s}$

$hc = 1240 \, \si{eV} \dot \si{nm}$

$e = \num{1.60 e-19} \, \si{C}$

$1 \, \si{u} = \num{1.66 e-27} \, \si{kg}$

$1 \, \si{u} = 931 \, \cfrac{MeV}{c^2}$

$c = \lambda f$

$E = hf$

$E = mc^2$

$\lambda = \cfrac{h}{p}$

$K_{max} = hf - \phi$

Trigonometry

$sin\theta = \cfrac{opposite}{hypotenuse}$

$cos\theta = \cfrac{adjacent}{hypotenuse}$

$tan\theta = \cfrac{opposite}{adjacent}$

$a^2 + b^2 = c^2$