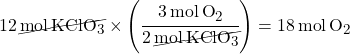A balanced equation is like a recipe. A recipe tells you how much of each ingredient to put in a cheesecake (or whatever). A balanced equation tells you how many of each molecule are involved in the reaction.
Let’s say a cheesecake recipe takes four cream cheese, three eggs, and one cup of sugar. It’s a balanced equation for cheesecake:
![]()
Food Ratio Problem 1: What if you need to make 5 cheesecakes? How many packages of cream cheese do you need to buy?
Answer: You need four cream cheese for every one cheesecake. You can write that ratio as a fraction:
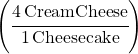
If this was a chemistry problem that you couldn’t do in your head, you would multiply the amount of cheesecake you want by this fraction to get the answer:
(Known Amount) x (Mole Ratio) = Answer
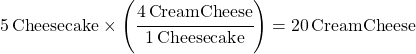
You need 20 packages of cream cheese.
This was setup to make “Cheesecake” units cancel out on the bottom of the mole fraction like this:
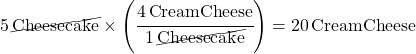
Here’s another type of problem: let’s say I have 24 packages of cream cheese. What’s the right number of eggs to go with 24 packages of cream cheese?
Food Ratio:
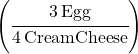
This time cream cheese goes on the bottom since we want it to cancel out when we calculate the answer:
(Known Amount) x (Mole Ratio) = Answer
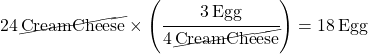
The math involved is simply this: 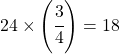
Mole Ratios / Chemical Reaction Recipes
Coefficients in a balanced chemical equations show mole ratios.
Example Balanced Equation:
![]()
The “2” in “2KClO3” is the first coefficient in this equation.
Mole Ratio Example Questions
Example 1: If 12 moles of KClO3 are used up, how many moles of O2 are produced?
Mole Ratio:
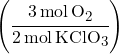
-
- We have KClO3 on the bottom since so it will cancel out.
- O2 is on top since that’s what we want to calculate.
- The “3” in “3O2” comes from the balanced equation.
- The “2” in “3KClO3” comes from the balanced equation.
-
(Known Amount) x (Mole Ratio) = Answer