Solving problems involving two objects connected by strings requires some new strategies.

Example

m₁ = 8 kg
m₂ = 3 kg
The acceleration of each block is 2.5 m/s².
Neglect friction (Friction force ≈ 0).
Calculate the tension forces T1 and T2.

Strategies

1) You can draw three different free body diagrams for this problem. For each diagram, you can write a net force equation.

a) Diagram of all forces acting on the m₁ block

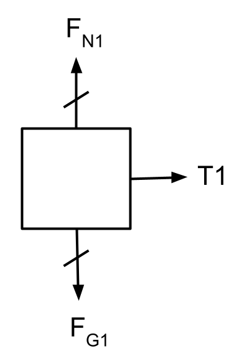
Net Force Equation:
F_net1 = T1

Notice that T2 does not appear in this diagram, because T2 is not connected to the m₁ block.

b) Diagram of all forces acting on the m₂ block

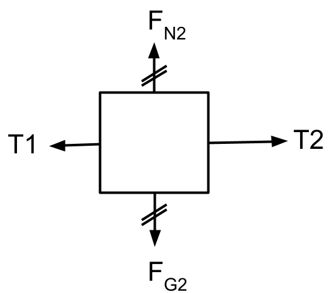
Net Force Equation:
F_net1 = T2 − T1

Note that T2 has to be more than T1, because the T2 string is indirectly pulling on both blocks, while the T1 string is only pulling one of them.

c) Diagram of all forces acting on the entire system
(Treat both blocks like a single object with total mass m₁+m₂)

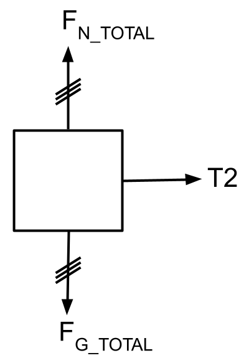
Net Force Equation:
F_net = T2

Notice that the T1 tension force does not appear in this diagram. It internally cancels out and does not affect the net force of the combined two block system.

2) Use F_net = ma equation for any of the free body diagrams.

Be careful! You need to use a different mass in each case, and the net forces will be different in each case.

Consider that the net force needed to accelerate one of the blocks is less than the net force needed for the combined two block system (more mass = more force needed).

Solution

i) It’s easier to start with the free body diagram for m₁, because it has horizontal forces on it.

F_net1 = ma = (8 kg)(2.5 m/s²) = 20 N

For this block, we already knew that F_net = T1.
Therefore, T1 = 20 N.
(see free body diagram equation above)

ii) We can now use this value with the m₂ free body diagram and force equation.

F_net2 = ma = (3 kg)(2.5 m/s²) = 7.5 N

Using the net force equation from the m2 free body diagram:
F_net1 = T2 − T1
7.5 N = T2 – 20 N
T2 = 27.5 N

The problem is now solved. Let’s also look at an alternate solution:

iii) We can instead start by looking at the overall system free body diagram.
For the entire system, mass = 8 kg + 3 kg = 11 kg.

F_net = ma = (11 kg)(2.5 m/s²) = 27.5 N

Use our net force equation from the overall free body diagram:
F_net = T2
F_net = 27.5 N

We get the same result. If we continue by plugging this value into our m2 force equation (F_net1 = T2 − T1), we can once again calculate that F_net1 = ma = 20 N and T1 = 7.5 N.

Summary

• Draw free body diagrams for each object, and also a free body diagram for the entire system as a whole.
• Write a net force equation to go with each diagram.
• Calculate F_net = ma for each diagram, remembering that mass and net force are different in each one.