Position, Velocity, and Acceleration

Position: location of an object relative to something else

  • distance units (m)
  • variable name is “x“
  • Similar to distance variable in equations

Velocity: rate of change of position

  • Similar to speed
  • distance covered in a given amount of time
  • distance per time units (m/s)

Velocity is the slope of a position vs time graph:

v = slope = \frac{\Delta x}{\Delta t}

v = \frac{(x_2-x_1)}{(t_2-t_1)} = \frac{(\SI{120}{m}-\SI{20}{m})}{(\SI{8}{s}-\SI{0}{s})} = \frac{\SI{100}{m}}{\SI{8}{s}} = \SI{12.5}{m/s}

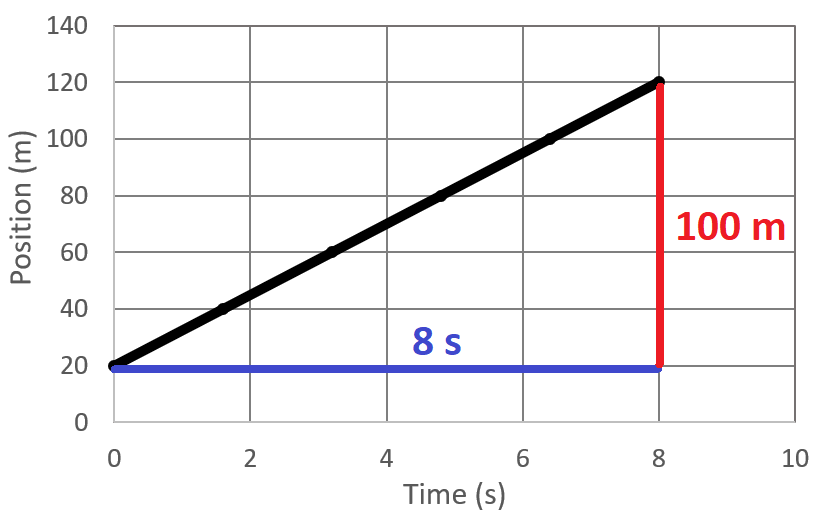
Where:

  •  v = velocity (m/s)
  •  x = position (m)
  •  Δx = change in position = x2 – x1
  •  t = time (s)
  •  Δt = change in time = t2 – t1

The equation for velocity is the same as the slope equation for a position vs time graph: change in distance over change in time.

Acceleration: rate of change of velocity

  • how fast velocity is changing
  • velocity per time units (m/s2)

Acceleration is the slope of velocity vs time graph:

a = slope = \frac{\Delta v}{\Delta t}

a = \frac{(v_2-v_1)}{(t_2-t_1)} = \frac{(\SI{10}{m/s}-\SI{2}{m/s})}{(\SI{4}{s}-\SI{0}{s})} = \frac{\SI{8}{m/s}}{\SI{4}{s}} = \SI{2}{m/s^2}

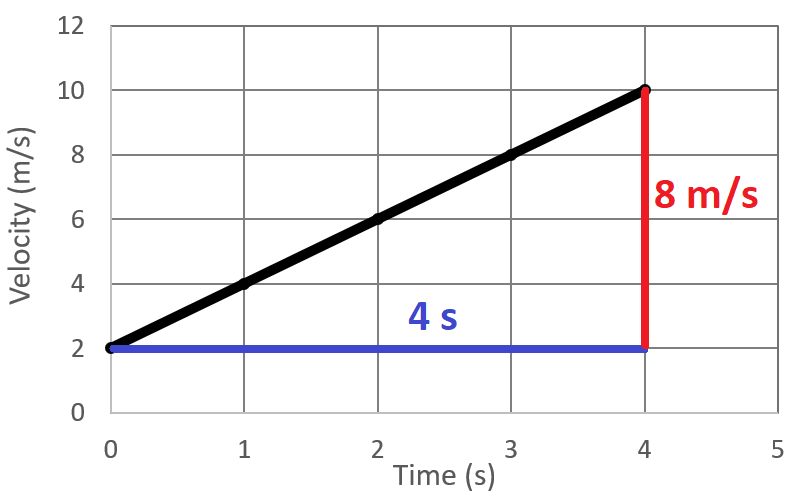
Where:

  • a = acceleration (m/s2)
  •  v = velocity (m/s)
  •  Δv = change in velocity = v2 – v1
  •  t = time (s)
  •  Δt = change in time = t2 – t1

The acceleration equation is the same as the slope equation or a velocity vs time graph: change in velocity over change in time.