Circular Motion – Centripetal Acceleration

Circular Motion – Velocity and Acceleration

When an object moves in a circular path, its velocity is tangent to the circle.

In order for an object to move in a circular path, its acceleration must be toward the center of the circle.
(centripetal means “toward the center”)

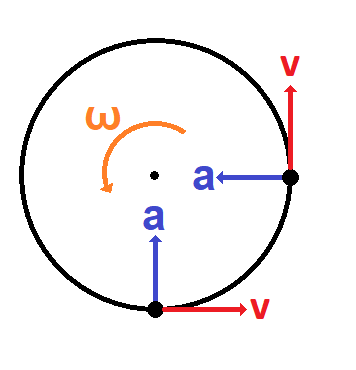
The “ω” symbol above is the Greek letter omega.
ω = angular velocity (revolutions / sec)

Centripetal Acceleration Equation

a_c = \cfrac{v^2}{r}

ac = centripetal acceleration (m/s2)
v = tangential velocity (m/s)
r = radius of circular path (m)

Speed / Velocity

Recall that velocity is a vector: it has both magnitude (amount) and direction. Speed is a scalar (no direction – only an amount).

An object can move in a circle at constant speed, yet it is still accelerating. This is because its direction is constantly changing.

The centripetal acceleration equation above calculates how much an object has to keep accelerating to continue moving in a circular path.

Centripetal Force

A force is needed to make an object accelerate and continue moving in a circle.

Example 1: If you spin an object around in a circle on a string, the string pulls the object toward the center of the circle. In this case, the centripetal force equals the tension force in the string.

Example 2: A planet orbiting a star in a circular path is kept in its orbit by the force of gravity from the star. The gravitational force from the star pulls the planet toward the center of the circle. In this case, the centripetal force equals the gravitational force.

Example 3: A car driving around a circular turn has a centripetal force pointing toward the center of the road’s circular arc. The acceleration force is from the lateral (sideways pointed) friction of the tires on the road. Centripetal force equals friction force in this situation.

Calculating Centripetal Force

You can combine Newton’s 2nd Law of Motion with the centripetal force equation to calculate a centripetal force, Fc.

F_{net} = ma

a_c = \cfrac{v^2}{r}

Combining the two equations above, and assuming that the centripetal force equals the net force in a simple situation, we get the following equation:

F_c = \cfrac{mv^2}{r}

Where:
Fc = Centripetal Force (N) – can be tension, gravity, friction, or other type of force depending on the situation
m = mass of the object moving in a circular path (kg)
v = tangential velocity of the object (m/s)
r = radius of the circular path (m)