Squared Units | NemoQuiz

Example Problem: convert 34 km² to m².

To convert squared units, you have to square the conversion factor to get the units to cancel out properly. The units AND the numbers get squared.

$\left(\cfrac{\SI{1000}{m}}{1 \, km}\right)^2 = \left(\cfrac{\SI{1000000}{m^2}}{1 \, km^2}\right)$

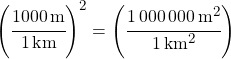
Solution:

$\cfrac{34 \, \cancel{km^2}}{1} \times \left(\cfrac{\SI{1000000}{m^2}}{1 \,\cancel{ km^2}}\right) = \SI{34000000}{m^2}$

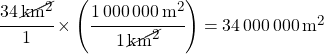
Notice that you have km² on top and bottom, and it cancels out properly.

Wrong Solution:

$\cfrac{\SI{34}{km^2}}{1} \times \left(\cfrac{\SI{1000}{m}}{\SI{1}{km}}\right) = \SI{34000}{km.m}$

If you don’t square the conversion factor, it won’t work since km² and km don’t cancel out $\left(\frac{\si{km^2}}{\si{km}}=\si{km}\right)$ . Also, your final units don’t end up as m² since you only multiplied by m¹ in the conversion factor. That’s why the final area units are “kilometer meters” in this wrong solution.

Another Look:

If you prefer, you can think of the solution in this way.

$\cfrac{\SI{34}{km^2}}{1} \times \left(\cfrac{\SI{1000}{m}}{\SI{1}{km}}\right) \times \left(\cfrac{\SI{1000}{m}}{\SI{1}{km}}\right) = \SI{34000000}{m^2}$

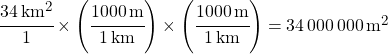
Multiplying by the conversion factor twice is the same as multiplying by a squared conversion factor. Either way, it cancels out km² and leaves you with m².

<– Previous: Multiple Steps