Dimensional Analysis

Why should I care about dimensional analysis?

Quick: if you’re converting from kilojoules to Joules, do you multiply by 1000 or divide by 1000? If you use dimensional analysis correctly, you will never screw that up. That’s why.

Equivalence Statement: an equation showing how two different units are related

Example:
$\SI{1}{kg}=\SI{1000}{g}$

Conversion factor: fraction made from an equivalence statement.

Examples:

$\left(\cfrac{\SI{1}{kg}}{\SI{1000}{g}}\right) or \left(\cfrac{\SI{1000}{g}}{\SI{1}{kg}}\right)$

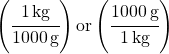
•any conversion factor equals one, because numerator equals denominator

•multiplying by a conversion factor is just multiplying by one; it doesn’t change the original quantity

Using Conversion Factors

To convert units, just multiply the original quantity by a conversion factor. Choose a conversion factor carefully so your old units will cancel out as shown below.

Example Question: Convert 11.7 kg to grams.

Solution:
$\boxed{11.7 \, \cancel{kg} \times \left(\cfrac{\SI{1000}{g}}{1 \, \cancel{kg}}\right) = \SI{11700}{g}}$

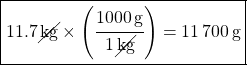
Choose the 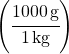$\left(\cfrac{\SI{1000}{g}}{\SI{1}{kg}}\right)$ conversion factor, because it has kg on the bottom – this causes kg to cancel out.

1000 appears in the top of the fraction, so that means you multiply the original amount by 1000. If it was in the bottom, you would divide by 1000 instead.

Example Wrong “Solution.” Here’s what happens if you put kilograms on top in your conversion factor:

$11.7 \, kg \times \left(\cfrac{\SI{1}{kg}}{\SI{1000}{g}}\right) = 0.0117 \, \cfrac{kg^2}{g}$

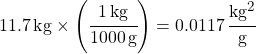
Now instead of canceling out, your kilograms multiply to become $\si{kg^2}$ . After dividing by the grams on the bottom, you end up with silly looking $\si{kg^2/g}$ units. That’s bad; you only want grams left at the end.

Another Wrong “Solution”:

$11.7 \, \cancel{kg} \times \left(\cfrac{\SI{1}{g}}{1000 \, \cancel{kg}}\right) = \SI{0.0117}{g}$

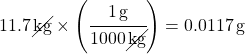
What’s wrong with that? Try to look at it and find the mistake.

…

The conversion factor is wrong; 1 gram (a paperclip) is not 1000 kilograms (a small car).

Do a reality check on your answers. If you’re converting from kilograms to grams, should your answer get bigger or smaller? Grams are much smaller, so it should take lots more grams to equal the 11.7 kg. Saying that 11.7 kg = 0.0117 g is like saying your dog has the same mass as a bread crumb.

<– Previous: Metric / Next: Multiple Steps–>